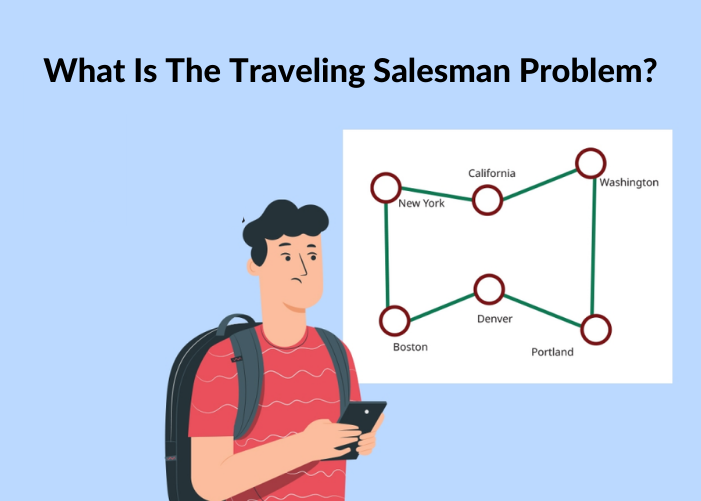
The Traveling Salesman Problem, also known as the Traveling Salesperson Problem or the TSP, is a well-known algorithmic problem in computer science. It consists of a salesman and a set of destinations.
The salesman has to visit each of the set of destinations, starting from a particular one and returning to the same destination.
Let us take a deep dive into what the challenge of the Traveling Salesman Problem is and how the TSP solutions can help in optimizing last-mile deliveries.
The Traveling Salesman Problem:
- The Traveling Salesman Problem was first formulated in 1930 by Merrill M. Flood, who looked to solve a school bus routing problem.
- It is one of the most intensively studied computational problems in optimization, used as a benchmark for many other optimization methods.
- The Traveling Salesman Problem (TSP) refers to the challenge of determining the shortest yet most efficient route for a traveling salesman to take to visit a list of specific destinations.
- The goal is to find the shortest route from a set of different routes to minimize the total distance traveled and the travel cost.
- The TSP is classified under combinatorial optimization problems known as “NP-complete.” It is classified as “NP-hard” because of two reasons:
- There are no quick solutions.
- The complexity of calculating the most optimum route increases when you add more destinations to the TSP.
- You can solve the TSP by analyzing every round-trip route to determine the shortest one.
- As the number of destinations increases, the corresponding number of routes increases exponentially. This exponential increase surpasses the computational capabilities of even the fastest computers.
- A set of ten destinations alone can have more than 300 thousand permutations and combinations of routes. A set of 15 destinations can have more than 87 billion possible routes.
- The Travelling Purchaser Problem (TPP) and the Vehicle Routing Problem (VRP) are generalizations of the TSP.
- The TSP has several applications, including planning and logistics.
Most Popular Solutions for the Traveling Salesman Problem:
- The Brute-Force/Naive Approach:
- The Brute-Force Approach calculates and compares all possible permutations of routes to find the shortest unique solution.
- The steps involved in solving the TSP using the Brute-Force Approach include:
- Calculating the total number of routes
- Drawing and listing all possible routes
- Calculating the distance traveled in each route
- Choosing the shortest route, which is the optimal solution.
2. The Branch-and-Bound Method:
- The Branch-and-Bound method involves breaking the problem into a series of sub-problems, each of which may have several possible solutions.
- The solution selected for one sub-problem may affect the possible solutions of subsequent sub-problems.
- The steps involved in solving the TSP using the Branch-and-Bound Method are as follows:
- Choose a start node and then set bound to a high value, say infinity.
- Select the cheapest arch between the unvisited and current node and then add the distance to the current distance.
- Repeat the process until the current distance is less than the bound.
- Then add up the distance so that the bound equals the current distance.
- Repeat this process until all the arcs are covered.
3. The Nearest Neighbor Method:
- This method is perhaps the simplest method to solve the TSP
- This method involves always visiting the nearest destination and then going back to the first destination when all other destinations are visited.
- The steps involved in solving the TSP using the Nearest Neighbor method are as follows:
- Choose a random destination
- Look for the nearest unvisited destination and go there.
- Once all destinations are visited, the salesman must return to the first destination.
4. Recent Solutions by Academics:
- Zero Suffix Method solves the classic symmetric TSP
- Biogeography‐based Optimization Algorithm solves the problem of optimization using the animals’ migration strategy.
- The African Buffalo Optimization Algorithm is derived from careful observation of the African buffalos.
- Meta-Heuristic Multi Restart Iterated Local Search (MRSILS) is more efficient than the Genetic Algorithms when clusters are used.
- Multi-Objective Evolutionary Algorithm solves multiple TSPs based on NSGA-II.
- Multi-Agent System solves the TSP of N cities with fixed resources.
Real-Life Solutions for The Last-Mile Delivery Problem:
Efficient solutions found through the Traveling Salesman Problem help to optimize and minimize the cost of last-mile deliveries.
These solutions help delivery businesses find a set of routes or paths to reduce delivery costs. The delivery problem domain involves a set of warehouse locations, delivery locations, and several delivery vehicles.
An efficient routing and delivery optimization software can provide the best solutions to logistic companies.
Are you ready to implement real-time routing and last mile route optimization software to plan your routes quickly and efficiently?